Vehicle Road Load
The force required to move a vehicle is a strong function of vehicle speed, road slope and acceleration. If we assume we are operating at a steady speed and on a flat road with no significant head or tail wind then the force required to operate the vehicle reduces to two main factors: rolling resistance and aerodynamic resistance. At low speeds, say below 30 kph, rolling resistance dominated. At higher speeds aerodynamic forces dominate. The magnitude of the forces depends on several factors such as vehicle weight, size and aerodynamic coefficient of drag (more explained below). In general high-speed operation can be approximated by a force proportional to the speed of the vehicle squared:
Force = K Speed2
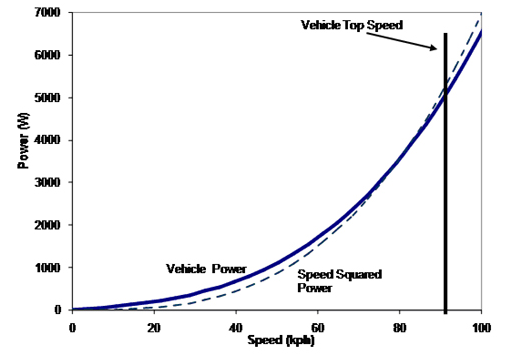
The coefficient K is adjusted so that the force is equal to the actual force at the desired speed of operation. As this is an approximation the “speed squared” load will not be exactly the same as the actual vehicle load, but it may be close enough for some testing near the speed where the loads match. In the below the actual vehicle load and speed squared load are graphed as a function of vehicle speed for a small motorcycle. The loads match at a speed of 80kph, and the vehicle tops speed is 93kph. This speed squared load might be appropriate for testing vehicle performance in the range of 65 to 95 kph.
Force - Torque
The force to drive the vehicle is transmitted through the drive wheels. The torque on the wheels can be calculated from the force by multiplying by the tire radius. Keeping things in SI units (Newtons for force, meters for radius, Nm for torque) makes the calculation simple:
Torque = Force x Radius
To determine the torque at the engine you need to know the gearing ratio from the wheels to the engine. This is typically on the order of 10, depending on which gear is selected. In general the engine is rotating at a relatively high speed, say 4,000 rpm, and the wheels are rotating at a much lower speed, perhaps 500 rpm. The torque of the engine is thus less than the torque at the wheels:
Torque (engine) = Torque (wheels) / Gear Ratio
Or in terms of speed:
Speed (engine) = Speed (wheels) x Gear Ratio
One thing we have neglected here is tire and transmission losses. The gearing system and tires are not 100% efficient, therefore some of the energy transmitted to them is lost and does not make it to the road. Generally the torque available at the wheels is 8 to 15% less than that available at the engine, mostly due to losses in the tire.
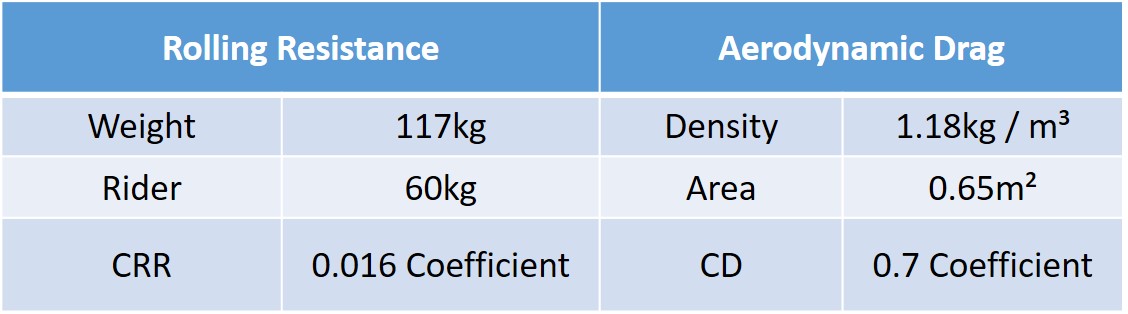
Rolling Resistance
The force required to roll a vehicle depends on the mass of the vehicle (including the driver and any load being carried) and the coefficient of rolling resistance (Crr). This coefficient depends strongly on the tires and road surface. Large low pressure tires with “knobby” tread patterns have higher Crr values, perhaps greater than 0.02, while well pressurized tires running on a concrete surface might have a Crr of below 0.014. Wheel bearings also contribute to the rolling resistance. The rolling resistance of a vehicle can be calculated from:
- Force (rolling) = Mass x Crr x 9.81 m/s2
- (9.81m/s2 is the gravitational acceleration constant)
Aerodynamic Resistance
The aerodynamic force on a moving vehicle depends on the frontal area of the vehicle (ie. the cross-sectional area as viewed from the direction of motion), the speed of the vehicle (squared) and the aerodynamic coefficient of drag (Cd). Aerodynamic cars may have Cd values below 0.3, while unfared motorcycles may have values of 0.7. The aerodynamic force on a vehicle can be calculated from:
- Force (aero) = 0.5 x Area x Cd x Velocity2 x 1.81 kg/m3
- (1.18 kg/m3 is the density of air at sea level. This can be reduced when simulating higher altitudes)
Force Power
The power required to move the vehicle at a steady speed on a flat, windless road is equal to the forces on the vehicle times the velocity:
Power = Force x Velocity
Putting the rolling resistance and aerodynamic forces together (and eliminating the “x” symbol for multiplication) we can calculate the steady-state power requirement as:
Power = (0.5 Area Cd Velocity2 1.81 + Mass Crr 9.81)
Velocity
For the small motorcycle of the previous figure we can calculate the power required to drive it as a function of speed from this equation. Using the parameters below we get the power as shown in the graph below. Again the “road load” power (same fit as previously mentioned) is plotted for reference. Despite the apparently large difference in the road load force, the power matched the actual vehicle power relatively well.